Temas
Estructuras dinamicas:
ventajas y desventajas:
-Mayor consumo de memoria porque por cada dato se almacena tambien una direccion para encontrar el siguiente.
-Ocupa la memoria a dedida que se requiere almacenamiento de datos.
-No requiere tiempo de pensamiento para elimianr datos. el eliminar se desocupa fisicamente el espacio de memoria.
-Para acceder al ultimo dato hay que pasar primero por todos los anteriores.
-El tamaño aumenta o disminuye de acuerdo a las operaciones de insercion o eliminacion
-Se recomiendad cuando el volumen de datos es considerable y se realizan muchas operaciones de insercion y eliminacion
 |
|---|
Estructuras estaticas:
ventajas y desventajas:
- Menor consumo de memoria para guardar datos.
- Posible subutilizacion de la memoria.
- Acceso directo a travez de un indice a los datos.
- Mayor velocidad en el recorrido de la estructura.
- Se recomiendan para almacenar pocos datos o cuando no haya muchas operaciones de insercion y eliminacion.
Listas enlazadas:
Estructura dinamica compuesta por un conjutno de nodos enlazados, con una referencia al nodo inicial. cada nodo esta compuesto por un atributo referencia dato y un atributo referencia nodo siguiente. el ultimo nodo de una lista enlazado tiene un valor null en el atributo de referencia al nodo siguiente que indica fin de la lista.
-ejemplo de lista enlazada:


- Para imprimir el nombre del tercer nodo :
- S.O.P (Estudiantes.getSig().getSig().getDato().getNombre());
- Para imprimir todos los nombres y codigos:

Tipos de listas enlazadas
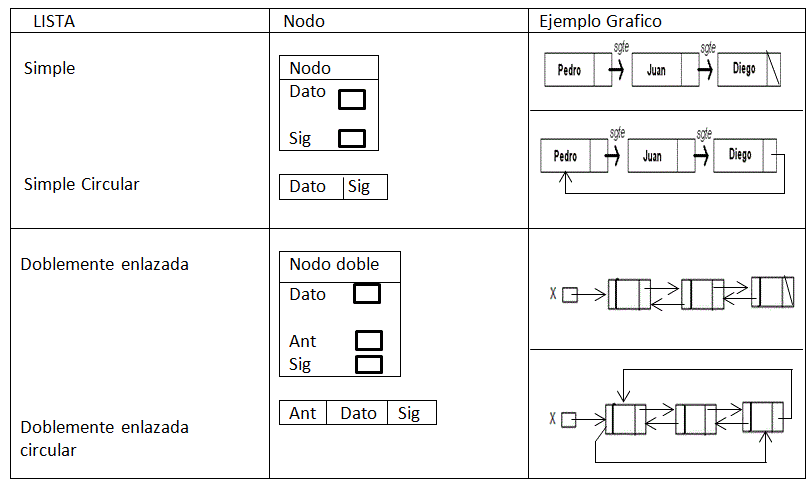
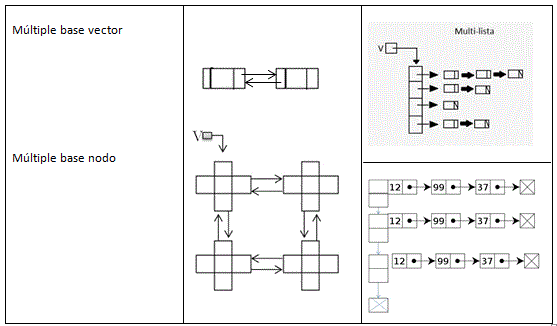
OPERACIONES EN LISTAS ENLAZADAS:
Para que esta estructura sea un lista enlazada, debe tener unos operadores asociados que permitan la manipulación de los datos que contiene. Los operadores básicos de una lista enlazada son:
-
Insertar: inserta un nodo con dato x en la lista, pudiendo realizarse esta inserción al principio o final de la lista o bien en orden.
-
Eliminar: elimina un nodo de la lista, puede ser según la posición o por el dato.
-
Buscar: busca un elemento en la lista.
-
Localizar: obtiene la posición del nodo en la lista.
-
Vaciar: borra todos los elementos de la lista
INSERTAR AL INICIO DE UNA LISTA :
-
SIMPLE:

-
PRIMERO SE CUMPLE LADO DERECHO DE LOS PARENTESIS EN LA DIRECCION 1010 Y LUEGO SE LE ASIGNA P ESE NEW NODO TENIENDO LA OTRA DIRECCION 4040
-
DOBLE :

-ELIMINAR AL INICIO DE UNA LISTA:
-
SIMPLE:

-
DOBLE :

Ejercicios y soluciones.

SOLUCION
c=a
d= a.getSig();
While (a! =null && b!= null){
a.setSig(b);
a=b.setSig(d);
b.setSig(d);
if( d!=null){
b=d.getSig();
d.setSig(a);
d= a.getSig();
}
}

SOLUCION
public class Lista <T>{ se le coloca <T> para que haga transferencia al nodo
private Nodo inicio;
private Nodo anterior;
private Nodo<T> actual;
private Nodo fin;
public Lista(){ aqui creamos el constructor el cual no es obligatorio ya que java lo crea por defecto
public boolean vacia(){
return inicio== null;
}
public void insertarInicio ( T dato String, Clave){
if (! vacia()) {
inicio= new nodo ( dato,clave,inicio)
}else{
inicio= fin= new Nodo ( dato, clave, null);
}
}
public void Listar() {
actual = inicio ;
while (actual != null){
system.out.print( actual.getDato());
actual= actual.getSig();
}
}
}
GRAFOS
2 de junio del 2015
Es un conjunto de nodos (vértices) y aristas (arcos), cada arista está formada por un par de nodos (x, y) pertenecientes al conjunto. Los grafos pueden ser dirigidos y no dirigidos, simples y multígrafos.

Arboles de expresiones
Los árboles de expresión representan el código en una estructura de datos en forma de árbol donde cada nodo es una expresión, por ejemplo, una llamada a método o una operación binaria como x < y.
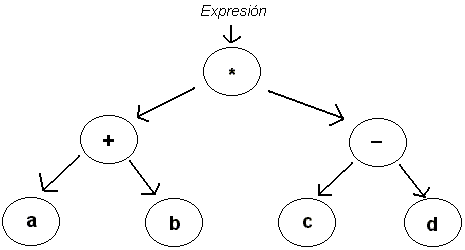
ÁRBOLES ABB: ÁRBOL BINARIO DE BÚSQUEDA
Árbol binario
la mayoría de los árboles binarios son de búsqueda. Un árbol binario no vacío, de raíz R, es un árbol binario de búsqueda si:
-
En caso de tener subárbol izquierdo, la raíz R debe ser mayor que el valor máximo almacenado en el subárbol izquierdo, y que el subárbol izquierdo sea un árbol binario de búsqueda
-
En caso de tener subárbol derecho, la raíz R debe ser menor que el valor mínimo almacenado en el subárbol derecho, y que el subárbol derecho sea un árbol binario de búsqueda.


ÁRBOLES BINARIOS BALANCEADOS : AVL
El árbol AVL toma su nombre de las iniciales de los apellidos de sus inventores, Georgii Adelson-Velskii y Yevgeniy Landis. Lo dieron a conocer en la publicación de un artículo en 1962, «An algorithm for the organization of information» («Un algoritmo para la organización de la información»).
Los árboles AVL están siempre equilibrados de tal modo que para todos los nodos, la altura de la rama izquierda no difiere en más de una unidad de la altura de la rama derecha o viceversa. Gracias a esta forma de equilibrio (o balanceo), la complejidad de una búsqueda en uno de estos árboles se mantiene siempre en orden de complejidad O(log n). El factor de equilibrio puede ser almacenado directamente en cada nodo o ser computado a partir de las alturas de los subárboles.
Para conseguir esta propiedad de equilibrio, la inserción y el borrado de los nodos se ha de realizar de una forma especial. Si al realizar una operación de inserción o borrado se rompe la condición de equilibrio, hay que realizar una serie de rotaciones de los nodos.




